Résoudre simplement les séries de dominos
Difficile d’évoquer les exercices de logique sans parler des suites de dominos. Il s’agit tout simplement de comprendre le fonctionnement d’de la série proposée et de la finir, ou du moins d’en trouver la suite. Les suites peuvent vous être présentées sous de multiples formes. Afin d’aborder les cas de figure les plus répandues dans les exercices de ce type, les dominos seront tous affichés en ligne (c’est la forme la plus utilisée).
Afin d’aborder les cas de figure les plus répandues dans les exercices de ce type, les dominos seront tous affichés en ligne (c’est la forme la plus utilisée).
Pour résoudre cet exercice de logique, une seule option : comprendre la règle de progression de la série. Autrement dit, de quelle manière passe-t-on d’un domino au suivant ?
Le principe de base à respecter : il faut raisonner en terme de cycle pour savoir quel domino succède à tel autre domino. Un exemple: en ajoutant 2 à 5, on arrive à…0. Pour ne pas vous tromper, dessinez les dominos ou écrivez simplement les valeurs.
Bien qu’il y ait un nombre incalculable de règles possibles, vous trouverez ci-dessous les principaux cas de figure que vous pouvez rencontrer dans ce type d’exercice. Les maîtriser devrait vous aider à vous en sortir haut la main !
La Superposition
Attention, il s’agit d’un cas de figure très spécifique et qui demande de bonnes capacités d’imagination. Il faut en effet imaginer que vous superposez des dominos et que vous voyez leurs points par transparence. Voyez plutôt:
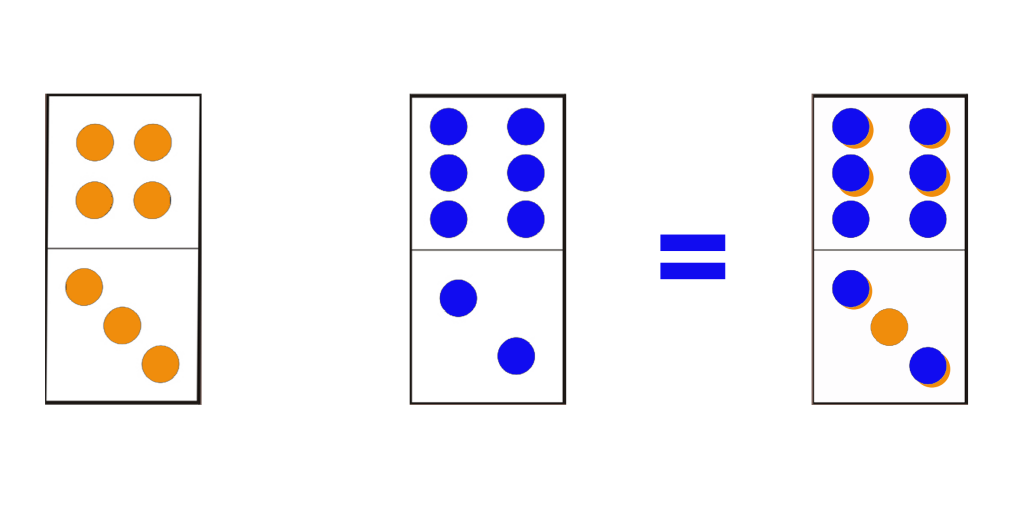
Les points des dominos se superposent!
Les Opérations
Dans ce type d’exercice, la valeur du dernier domino est donnée par une opération entre plusieurs autres dominos. Il vous suffit alors d’appliquer la même opération pour les dominos suivants pour finir la suite. Tout type d’opération peut être concerné:addition, différence, produit, quotient. Par exemple:
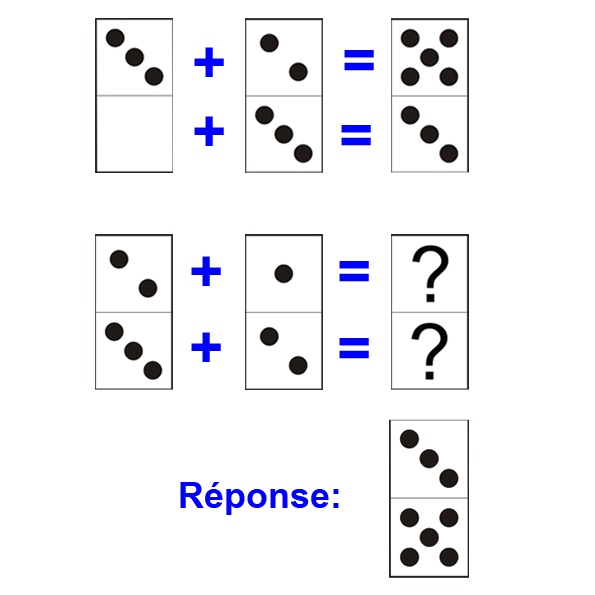
Exemple de somme : le troisième domino est le résultat de la somme des deux précédents
Progression en ligne
C’est le type de progression le plus abordable. Chaque moitié de domino croît ou diminue. Pas besoin donc d’être un expert en maths! Attention : la progression peut être différente sur la partie supérieure ou inférieure du domino (+1/-1, ou autre). On appelle une progression « croisée ».
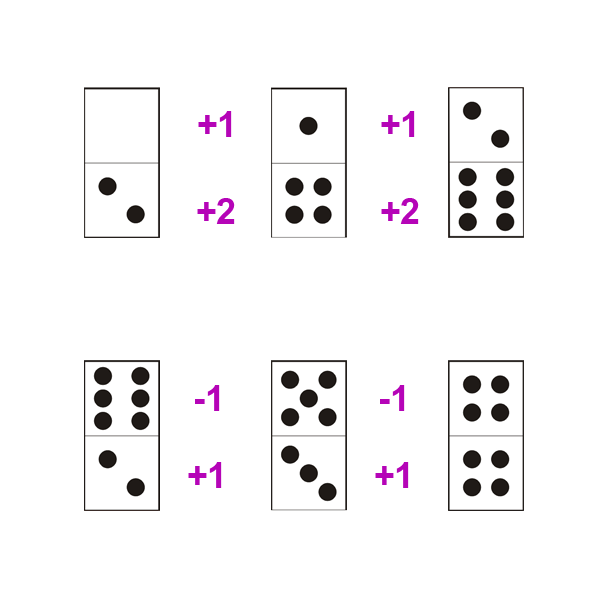
Exemples de progression
La Similarité
Il s’agit d’identifier un motif dans la série de dominos. Par exemple, une alternance entre 2 dominos qui se répètent, ou encore les mêmes dominos dans le désordre. Pour identifier ces motifs, il faut faire preuve d’un bon sens de l’observation. Un exemple:
Progression décroissante ou croissante en diagonale
C’est un cas de figure propre aux dominos, qui demande un peu d’attention. La règle demeure la même que pour une progression en ligne (les valeurs des dominos augmentent ou décroissent), mais la manière de lire la série est différente : la progression se fait en « dents de scie » ou en « Z ». 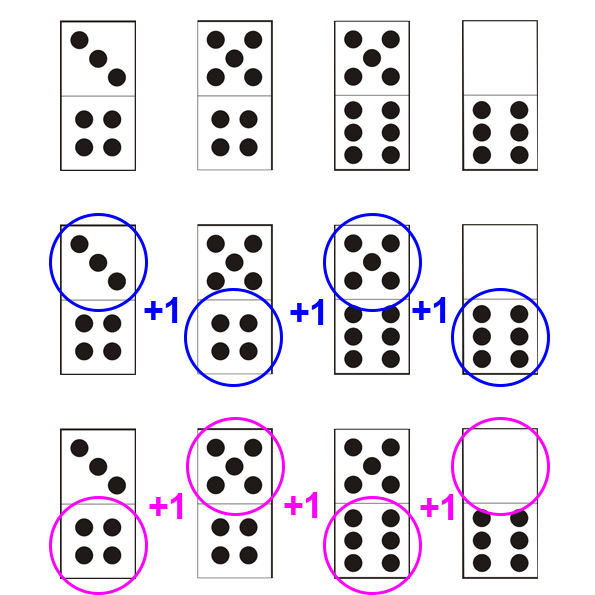
Et si vous trouvez ce cas de figure trop simple: les valeurs de chaque moitié de domino peuvent évoluer différemment !
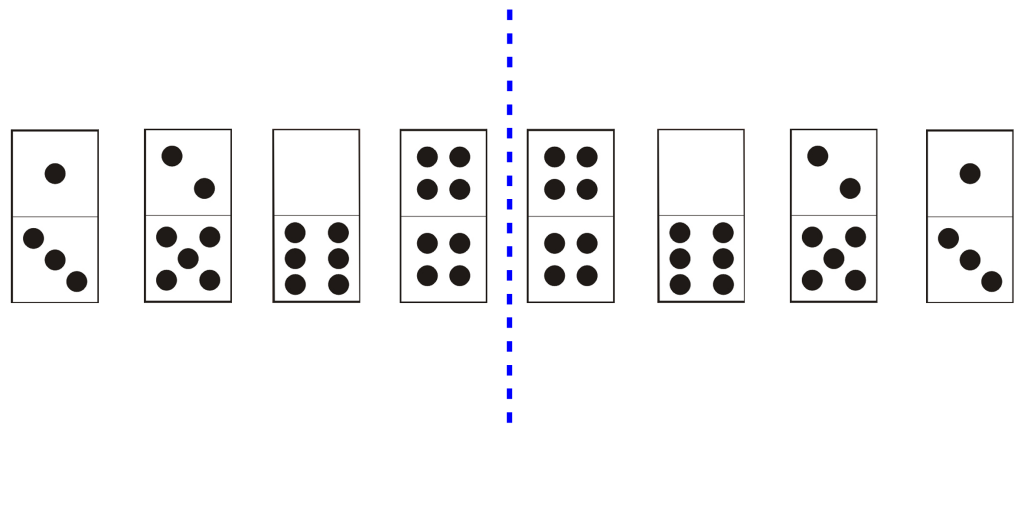
LaSymétrie
Votre capacité d’observation sera mise à l’épreuve dans cette règle logique.
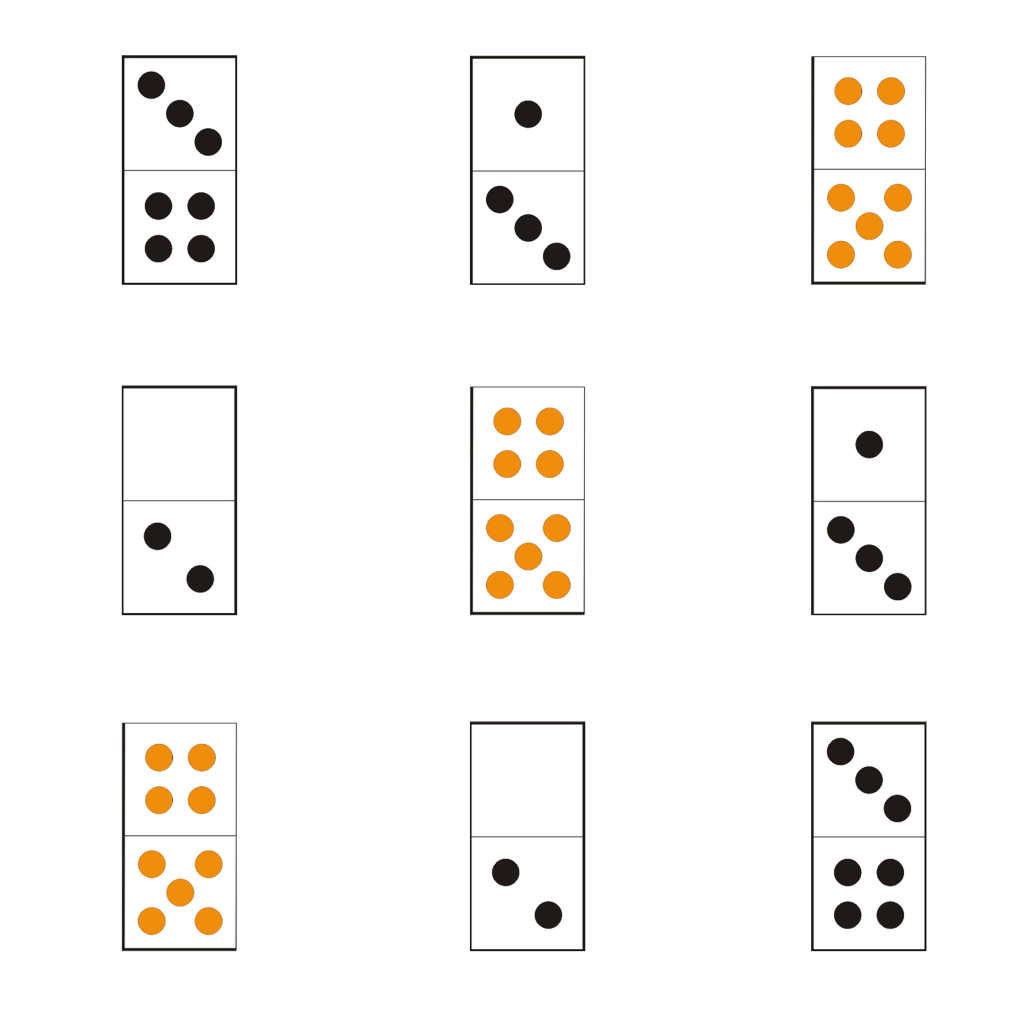
Cas de symétrie axiale, plus compliqué à repérer !
Ce tour d’horizon des séries de dominos est fini.
A vous maintenant de vous entraîner pour être prêt(e) le jour J!
Découvrir de quelle manière résoudre les autres types de tests d’aptitude.