Suites de Dominos : cas de figure les plus classiques
Les exercices de dominos font partie des incontournables des concours ou tests de recrutement. Voici comment se présente ce type d’exercice : une série de dominos vous est présentée, et vous devez comprendre la logique de l’exercice pour terminer la série. Les suites de dominos peuvent vous être proposées sous plusieurs formes. Afin d’aborder les cas de figure les plus répandues dans les suites, les dominos seront tous présentés en ligne (c’est la forme la plus répandue).
Afin d’aborder les cas de figure les plus répandues dans les suites, les dominos seront tous présentés en ligne (c’est la forme la plus répandue).
Pour résoudre cet exercice , il faut découvrir la règle interne de la série. Autrement dit, comment passe-t-on d’un domino au suivant ? De quelle manière les valeurs évoluent-elles ?
Une règle de base à connaître : il est impératif de penser en terme de cycle afin de comprendre quel domino succède à tel autre domino. Un exemple: en ajoutant 2 à 5, on arrive à…0. Pour vous aider, dessinez les dominos ou notez les valeurs.
Bien qu’il y ait une infinité de possibilités, voici les principaux cas de figure que vous pouvez rencontrer dans ce type d’exercice. Les maîtriser devrait vous aider à marquer un maximum de points sur ces questions !
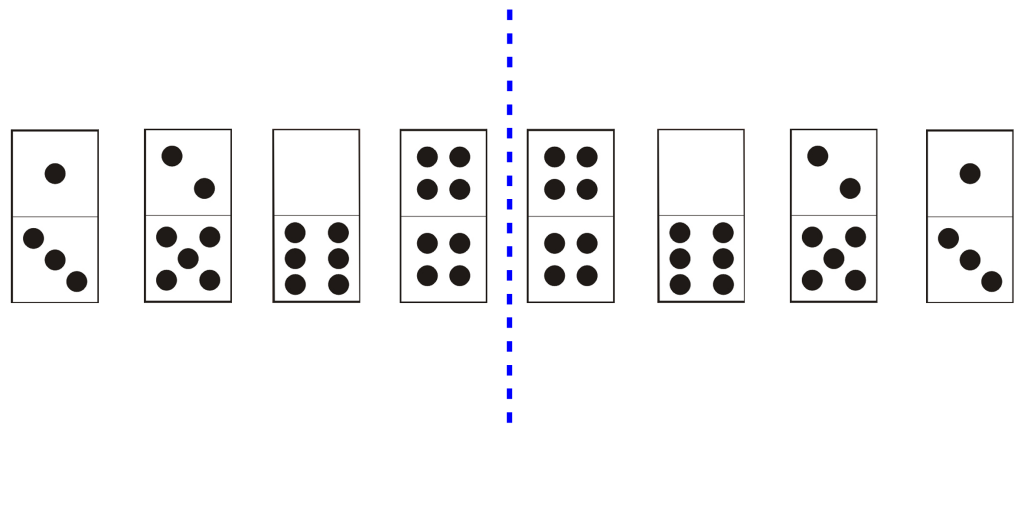
La Similarité
L’objectif est ici de repérer un “schema” dans la série de dominos. Par exemple, une alternance entre 2 dominos différents, ou encore les mêmes dominos dans le désordre. Pour identifier facilement ces répétitions, il faut posséder un sens aigu de l’observation. Ci-dessous un exemple:
Progression croissante ou décroissante en “Z”
C’est un cas de figure propre aux dominos, qui demande d’être particulièrement attentif. La base reste la même que pour une suite en ligne (les valeurs des dominos croissent ou décroissent), mais le sens de lecture est différent : la progression se produit en dents de scie ou en diagonale. 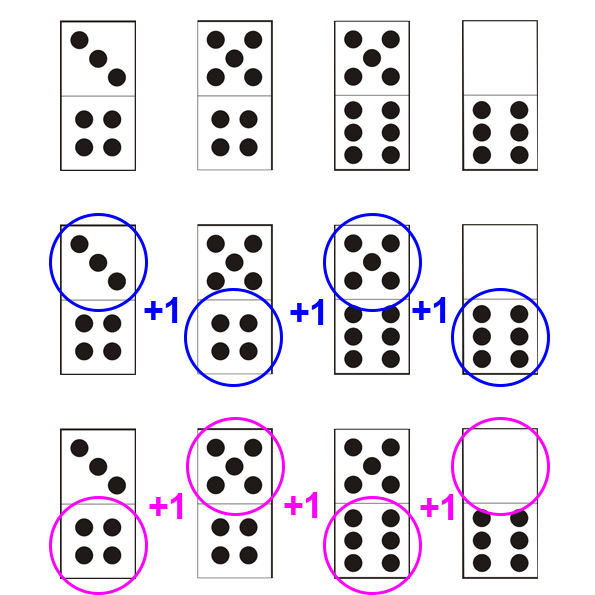
Et si vous trouvez ce cas de figure trop simple: la progression peut être croisée !
La Superposition
Il s’agit d’un cas de figure propre aux séries dedominos. Afin de bien comprendre comment fonctionne cette règle logique, il faut visualiser les dominos sont transparents, comme s’ils étaient en verre, et qu’on n’aperçoit que les points. En les superposant, on voit les points par transparence. Il s’agit probablement du cas de figure le moins facile à repérer!
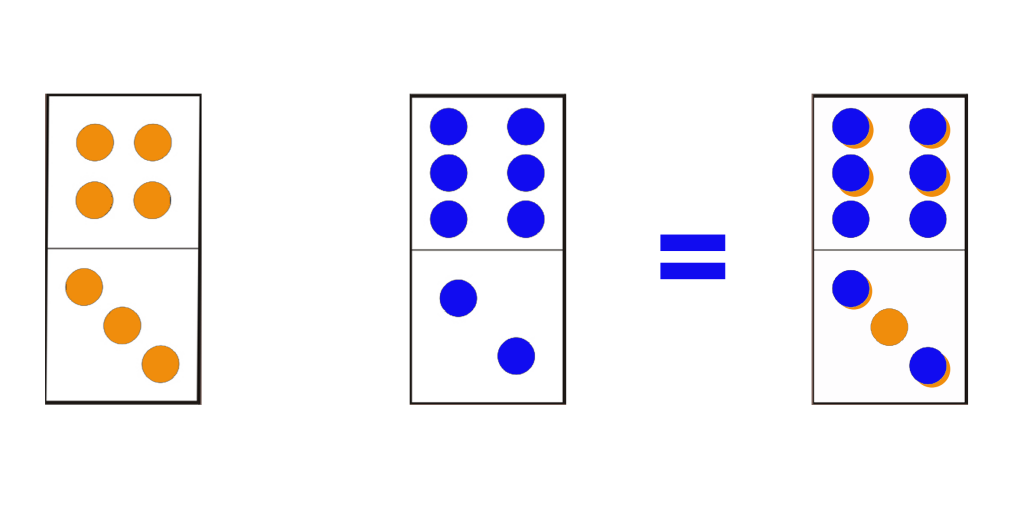
Les points des dominos se superposent, tout simplement!
Opérations
Dans ce type de suite, la valeur d’un domino est donnée par une opération entre plusieurs autres dominos. A vous de répéter la même opération pour résoudre l’exercice. Il peut s’agir d’une addition, d’une différence, d’un produit ou même d’une division. Par exemple:
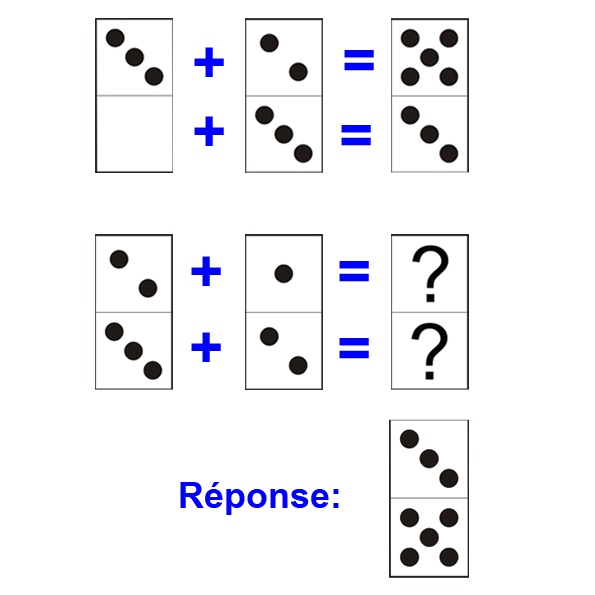
Exemple de somme : le troisième domino est le résultat de la somme des deux précédents
Symétrie
Si dans la plupart des cas il vous faudra effectuer des calculs pour comprendre de quelle façon s’enchaînent les valeurs, parfois il vous suffira d’observer attentivement l’exercice afin de repérer un cas de symétrie.
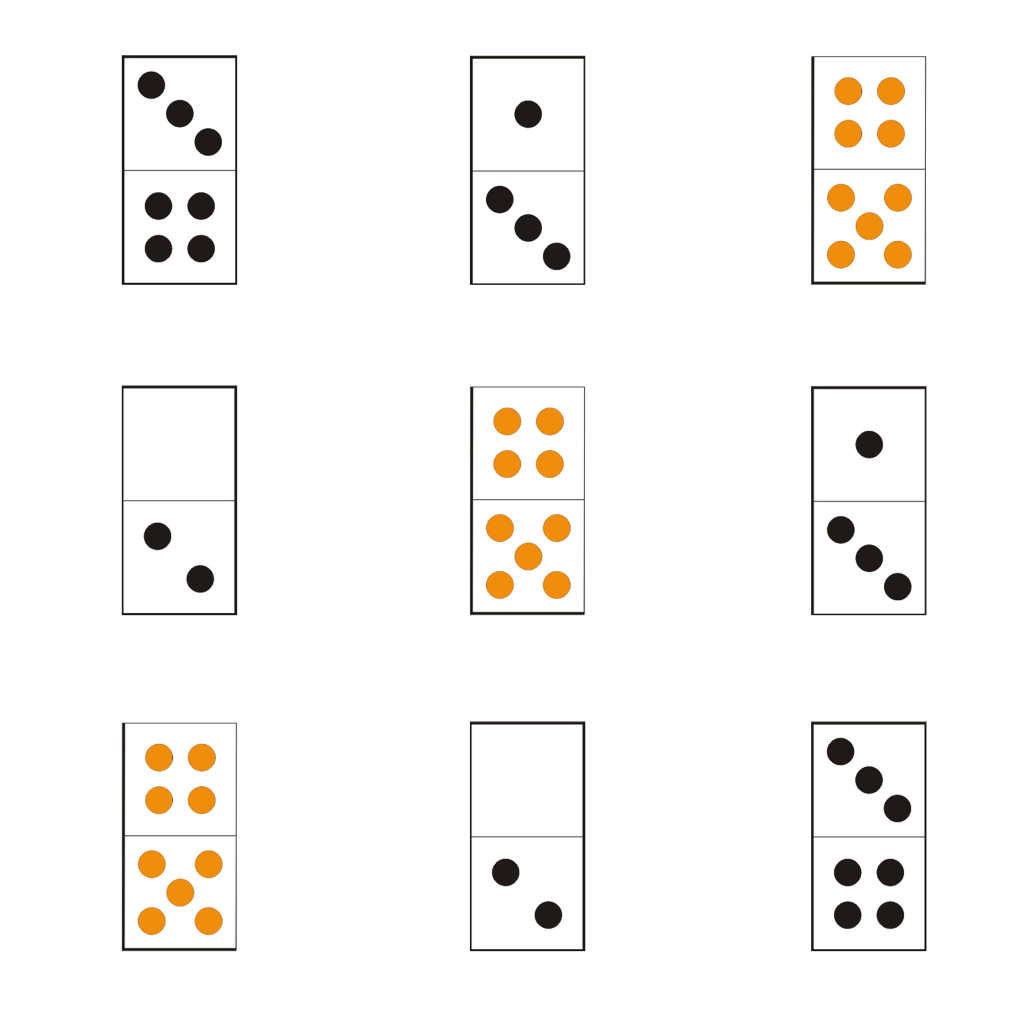
Une symétrie axiale,moins évidente à détecter !
Suite croissante ou décroissante
C’est le type de progression le plus utilisé. Chaque valeur croît ou diminue. Il suffit de savoir compter sur ses doigts ! Il est à noter que les valeurs peuvent croître ou décroître de façon différente en haut et en bas (+1/-1, ou autre). On nomme ce type de suite une progression “croisée”.
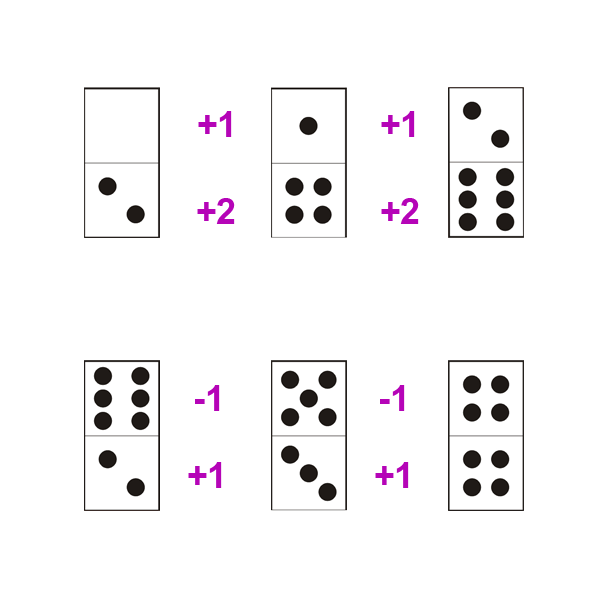
Exemples de progression
Voilà, c’est terminé pour les dominos.
Il ne vous reste plus qu’à vous entraîner !
Découvrez comment résoudre les autres types de tests d’aptitude logique.