Les dominos: comment les résoudre?
Difficile d’évoquer les tests de logique sans aborder le cas des séries de dominos. Il s’agit de comprendre la règle qui régit une série donnée et de la terminer, ou du moins d’en trouver la suite. Les suites peuvent vous être présentées sous de multiples formes. Afin de détailler les règles logiques les plus utilisées dans les tests de ce type, les dominos seront tous affichés en ligne (il s’agit de la forme la plus répandue).
Afin de détailler les règles logiques les plus utilisées dans les tests de ce type, les dominos seront tous affichés en ligne (il s’agit de la forme la plus répandue).
Pour réussir ce test logique, il est nécessaire de découvrir la règle interne de la suite. En d’autres termes, de quelle manière passe-t-on d’un domino à l’autre ? Comment les valeurs évoluent-elles ?
Le principe de base à connaître absolument : il est impératif de raisonner en terme de cycle pour savoir quelle valeur succède à tel autre domino. Un exemple: si on ajoute 2 à 6, on arrive à à …1. Pour ne pas vous tromper, dessinez les dominos ou notez les valeurs.
Bien qu’il y ait une infinité de possibilités, voici les principaux cas de figure que vous pouvez rencontrer dans ce type de tests de logique. Les maîtriser devrait vous permettre de vous en sortir haut la main !
Progression en ligne (croissante / décroissante)
C’est le type de progression le plus abordable. Chaque moitié de domino augmente ou décroît. Il suffit de savoir compter sur ses doigts ! Soyez néamnoins attentif: la progression peut être différente sur la partie haute et la partie basse du domino (+1/-1, ou autre). On parle alors d’une progression “croisée”.
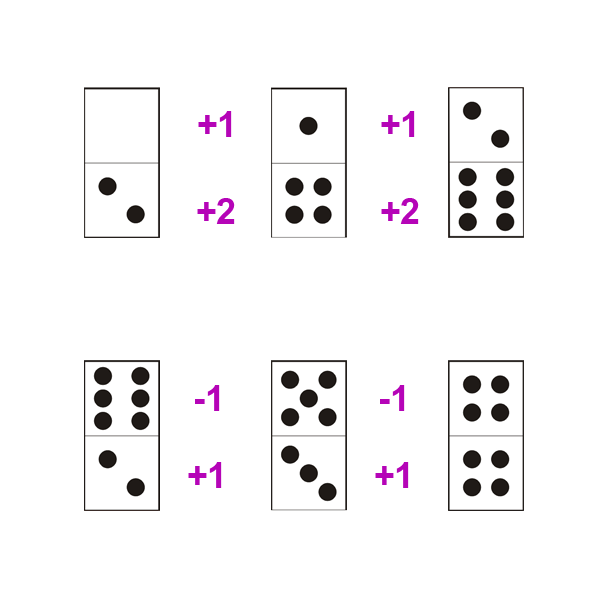
Exemples de progression
Progression décroissante ou croissante en diagonale
Il s’agit d’un cas de figure propre aux exercices de dominos, qui requiert une certaine attention. La base demeure la même que pour une suite en ligne (les valeurs croissent ou décroissent), mais le sens de lecture est différent : la progression se fait en “Z” ou en diagonale. 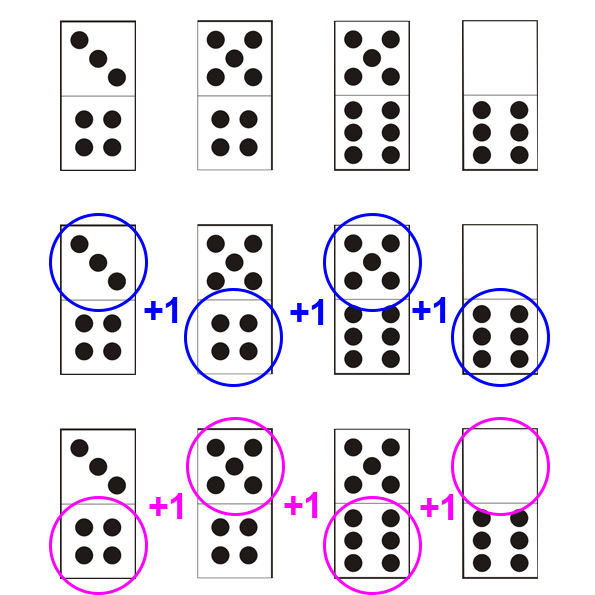
Une variante pour compliquer la question : les valeurs de chaque moitié de domino peuvent évoluer à un rythme différent !
Similarité
L’objectif est ici d’identifier un “schema” dans la série de dominos. Cela peut être une alternance entre 2 dominos différents, ou encore les mêmes dominos dans le désordre. Pour identifier facilement ces motifs, il faut posséder un bon sens de l’observation. Ci-dessous un exemple:
Opérations (addition, soustraction, multiplication, divisions)
C’est quand le dernier domino d’un exercice est le résultat d’une opération entre d’autres dominos. Il vous suffit alors de faire la même chose pour les dominos suivants pour résoudre la suite. Tout type d’opération peut être concerné:addition, différence, multiplications, divisions. Voilà quelques exemples:
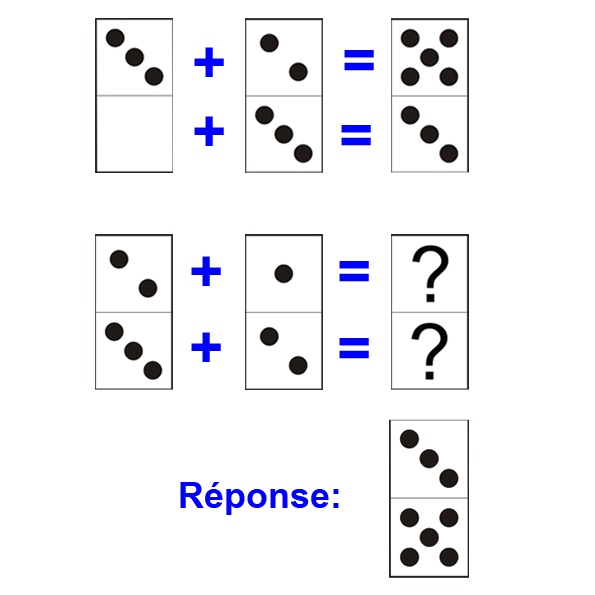
Exemple de somme : le troisième domino est le résultat de la somme des deux précédents
Symétrie
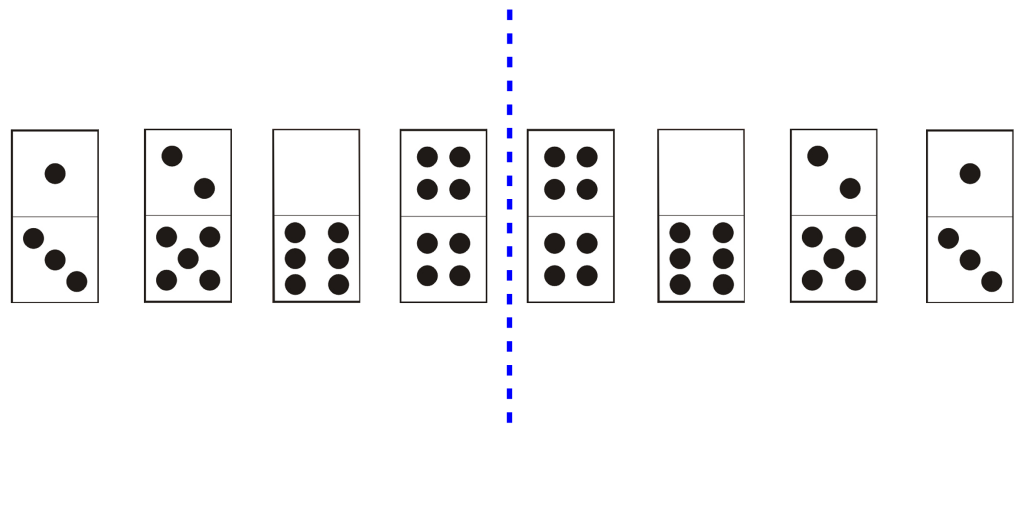
Il s’agit d’une cas de figure qui fait appel à votre sens de l’observation. Une symétrie peut vous « sauter » aux yeux, mais elle peut aussi être plus difficile à repérer.
Exemple de symétrie axiale, plus difficile !
La Superposition
Attention, il s’agit d’une règle d’enchaînement très particulière et qui exige de bonnes capacités d’abstraction. Il faut en effet imaginer que vous superposez des dominos et que vous pouvez voir les points par transparence. Un exemple:
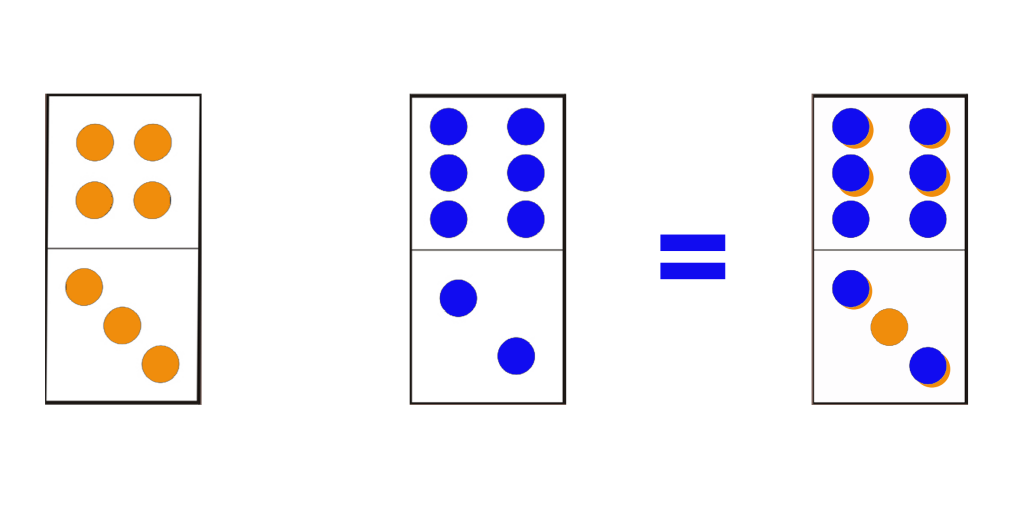
Les points des dominos se superposent!
Ainsi se termine cette revue détaillée des exercices de type Domino.
A vous maintenant de vous entraîner pour être prêt(e) le jour J!
Découvrez comment venir à bout des autres tests psychotechniques.